Table of Contents:
- Introduction
- What is Hooke’s Law?
- The Basics
- Stress and Strain
- Defining Stress
- Understanding Strain
- Hooke’s Law Equation
- Hookes law Formula
- Stress-Strain Diagram
- Point A – Proportionality Limit:
- Point B – Elasticity Limit:
- Point C – Flow Limit:
- Point D – Resistance Limit (Ultimate Tensile Stress):
- Point E – Breaking Limit:
- Conclusion
Introduction
Hooke’s law describes the relationship between stress and strain in a material, particularly in the context of linear elasticity. The stress-strain diagram is a graphical representation of this relationship, which helps us understand how a material behaves under mechanical loading. In the diagram, stress is plotted on the y-axis, and strain is plotted on the x-axis.
What is Hooke’s Law?
The Basics
Hooke’s Law is a fundamental concept in the field of physics and materials science, named after the renowned 17th-century scientist Robert Hooke. At its core, Hooke’s Law describes the linear relationship between the stress applied to a material and the resulting strain it undergoes. In simpler terms, it explains how materials deform when subjected to external forces.
Stress and Strain
Defining Stress
Before delving into the intricacies of Hooke’s Law, it’s essential to grasp the concepts of stress and strain. Stress is the measure of the internal resistance of a material to deformation when subjected to an external force. It is expressed in units of force per unit area, typically in Pascals (Pa).
Understanding Strain
Strain, on the other hand, is the measure of how much a material deforms when subjected to stress. It quantifies the relative change in size or shape of a material and is usually expressed as a dimensionless ratio or a percentage.
Hooke’s Law Equation
Hookes law Formula
Hooke’s Law can be mathematically represented by the simple equation:
F = k * ΔL
Where:
- F represents the force applied to the material.
- k is the material’s stiffness or the spring constant.
- ΔL is the change in the length of the material.
This equation elucidates the direct proportionality between the applied force and the resulting deformation.
Stress-Strain Diagram
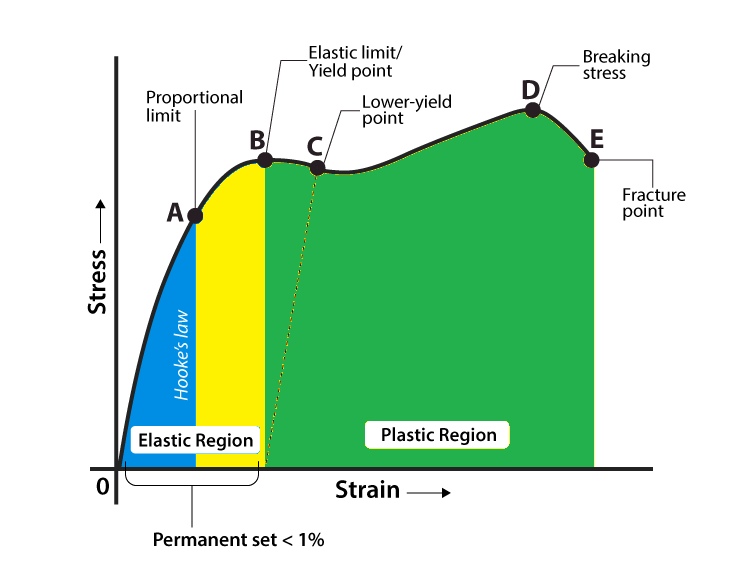
Now that we’ve established the basics, let’s dive into the heart of the matter – the stress-strain diagram. This graphical representation is a fundamental tool in understanding how materials respond to stress.
1. Point A – Proportionality Limit:
At point A, stress and strain are directly proportional to each other. This means that within this region, Hooke’s law holds true, and the material behaves elastically.
If the applied stress is removed at any point before reaching point A, the material will return to its original shape and dimensions with no permanent deformation.
2. Point B – Elasticity Limit:
Point B represents the limit of the elastic deformation region. Beyond this point, the material begins to exhibit plastic deformation, which means it undergoes permanent changes in shape and size even after the load is removed.
If the material is subjected to stress beyond point B and then unloaded, it will not return completely to its original shape; there will be some residual deformation.
3. Point C – Flow Limit:
Point C marks the beginning of the flow or yielding region. In this region, the material continues to deform plastically with an increase in strain, even if the applied stress remains constant.
The material’s ability to resist further deformation diminishes, and it flows or yields under the sustained load.
4. Point D – Resistance Limit (Ultimate Tensile Stress):
Point D represents the ultimate tensile stress or the maximum stress that the material can withstand before failure. Beyond this point, the material starts to neck down or narrow significantly as it approaches failure.
At the resistance limit, the material’s internal structure and bonds are significantly compromised, and it cannot sustain any additional load.
5. Point E – Breaking Limit:
Point E marks the point of material failure, where it ruptures or breaks. Beyond this point, the material can no longer support any stress, and it undergoes a catastrophic failure.
Conclusion
In conclusion, Hooke’s Law is a fundamental principle that governs the behavior of materials under stress. Understanding stress and strain, as well as interpreting stress-strain diagrams, is essential for engineers and scientists working with materials in various applications. By applying this knowledge, we can design and utilize materials more effectively and efficiently.
Understanding the stress-strain diagram is crucial for engineers and materials scientists to predict how a material will behave under different loading conditions and to design structures that can withstand anticipated stresses without failure. Different materials have different stress-strain behaviors, so studying these diagrams helps in selecting appropriate materials for specific applications
FAQs
Q1: Is Hooke’s Law applicable to all materials?
Hooke’s Law is primarily applicable to elastic materials, which return to their original shape after stress is removed. Some materials, like rubber, do not follow Hooke’s Law behavior.
Q2: What are the practical applications of stress-strain diagrams?
Stress-strain diagrams are widely used in engineering to determine material properties, design structures, and ensure the safety of various components.
Q3: Can materials exceed their ultimate tensile strength?
Materials can occasionally exceed their ultimate tensile strength under dynamic loading conditions, but this is typically not recommended, as it may lead to catastrophic failure.
Q4: How is Hooke’s Law used in everyday life?
Hooke’s Law principles are applied in various everyday items, including springs, elastic bands, and shock absorbers, to ensure their functionality and durability.
Q5: Are there materials that do not follow Hooke’s Law at all?
Yes, some materials, like glass and concrete, exhibit non-linear stress-strain behavior and do not follow Hooke’s Law.



![Read more about the article Storage Tank :: Inspection and Test Plan [ITP]](https://englogs.com/wp-content/uploads/2022/09/Inspection-and-Test-Plan-for-Storage-Tank-300x211.jpg)